遊び日記 • (過去記事転載)ライブラリに頼らずにニューラルネットワークを実装する

はじめに

本記事では、著書「ゼロから始めるDeep Learning」を参考に、Pythonで、ライブラリを極力使わずに 2層のニューラルネットワークを実装、MNISTの画像データの学習を実装していきます。

環境

CPU:第７世代intel corei7
OS:Windows10home
Language:Python3.6.5

各種関数の実装

ディープラーニングを実装する前に、実装に必要な要素をfunctionsというファイルにまとめます。また、ほとんどの関数でnumpyを使います。numpyは使ってもいいですよね？

import numpy as np

活性化関数

活性化関数は、各ニューロンへの入力を整形するのに用いる関数です。今回はシグモイド関数のみ使用していますが、ReLuも有名なので実装しました。

シグモイド関数

シグモイド関数は、

$$f(x) = \frac{1}{(1 + e^{-x})}$$

で表される、入力の値の0から1の間に収めるための関数です。これをそのまま実装します。

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

シグモイド関数の勾配

シグモイド関数の勾配を逆伝播で求めます。

まず、計算グラフで$f(x) = \frac{1}{(1 - e^{-x})}$をそのまま表現します。

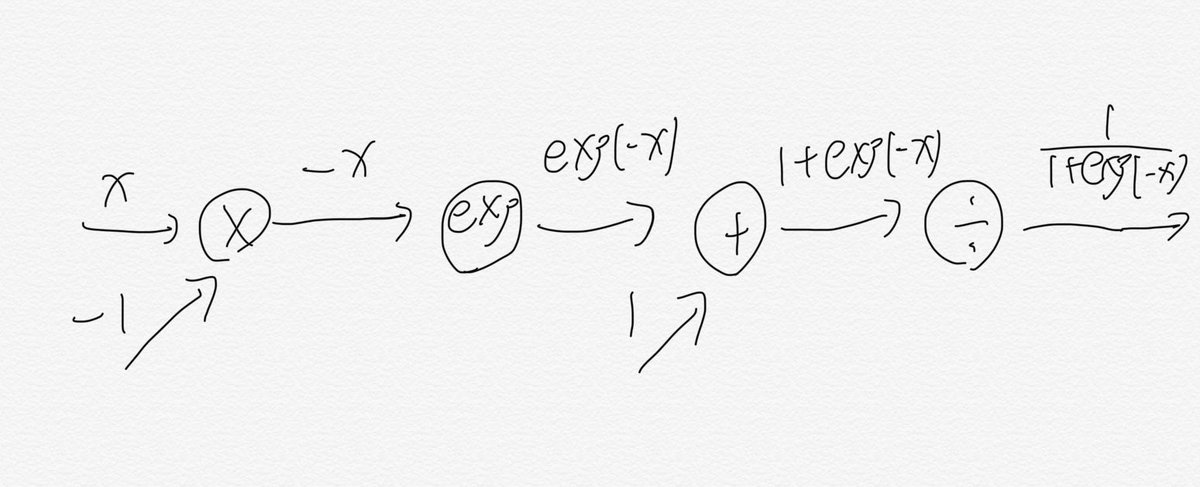
次に、$\frac{1}{(1 - e^{-x})}=y$とし、逆伝播していきます。

以上より、$f(x) = \frac{1}{(1 - e^{-x})}$の勾配は

$$\frac{\partial L}{\partial y}y^2\exp(-x)$$

これを整理して、 $$\frac{\partial L}{\partial y}y(1-y)$$ で表されることがわかりました。これをそのまま実装します。

def sigmoid_grad(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)

ReLu

Reluは、入力が0以下の時は0を、0より大きい時はそのままの値を返す関数です。

def relu(x):
    return np.maximum(0, x)

numpyのmaximumは、引数を２つ取り、値の大きいほうを返すメソッドで、0とreluの引数をmaximumで比較することでReLuを実装しています。

損失関数

損失関数は、学習の誤差、どれだけ間違えたかを出力します。勾配法によってこの値を小さくします。ニューラルネットワークの出力と教師データを引数にとり、その誤差を出力します。今回使うのは交差エントロピー誤差ですが、有名な二乗和誤差も実装してみました。

二乗和誤差

二乗和誤差は、

$$E = \frac{1}{2}\sum_{n}(y_k - t_k)^2$$

で表されます。誤差の二乗の和です。

def sum_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)

交差エントロピー誤差

交差エントロピー誤差は、

$$E = -\sum_{k}t_k \log{y_k}$$

で表されます。今回行うのはバッチデータに対する学習なので、

$$E = -\frac{1}{N}\sum_{n} \sum_{k}t_{nk} \log{y_{nk}}$$

のようにN個の訓練データの誤差平均を出すような形にします。

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)


    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

y(ニューラルネットワークの出力)の次元が１の場合は、データ一つあたりの誤差を計算するためにデータを整形しバッチの枚数で正規化します。 y[np.arrange(batch_size),t]は、各データの正解ラベルに対応するニューラルネットワークの出力を抽出します。今回はｔがラベル表現なので、このような形をとりました。また、y[np.arrange(batch_size),t]の値が０になった時、np.log(0)=-∞になってしまうので、それを避けるために1e-7のような微小な数を加えています。

出力層

恒常関数

恒常関数は、出力層の中でも、入力された値をそのまま返す関数です。主に分類問題で使います。実装も、

 def constant(x):
    return x

のように簡単です。

ソフトマックス関数

ソフトマックス関数は、主に回帰問題で使います。

$$y_k = \frac{\exp(a_k)}{\sum_{i=1}^{n}\exp(a_i)}$$ ここで、 $y_k$($k = 0,1,...$)は出力層のニューロン、 $a_k$($k=0,1,...$)は、出力層に対する入力層の各ニューロンです。分母を見ると分かる通り、全ての出力が、全ての入力から影響を受けます。

このままの形で使用すると、$a_k$の値が大きくなってくると簡単にオーバーフローを起こしてしまうので、任意定数$C$を用いて、

$$ \begin{aligned} y_k &= \frac{C\exp(a_k)}{C\sum_{i=1}^{n}\exp(a_i)} \\ &= \frac{\exp(a_k +\log{C})}{\sum_{i=1}^{n}\exp(a_i+\log{C})} \\ &= \frac{\exp(a_k+C')}{\sum_{i=1}^{n}\exp(a_i+C')} \end{aligned} $$

で対策します。 $C'$は、入力信号の中で最大の値を用いるのが一般的で、今回もそのように実装します。

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x)
    return np.exp(x) / np.sum(np.exp(x))

２層ニューラルネットワークの実装

TwoLayerNetというクラスの形で実装します。

import sys, os
import numpy as np
sys.path.append(os.pardir)  
from functions import *

numpyのほかに、親ディレクトリのファイルをインポートするための設定に必要なライブラリも使っていますが、本質から外れるので説明は省きます。上で実装した関数たちが入っているfunctionsファイルもインポートします。

次は、クラス本体です。

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):

        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y


    def loss(self, x, t):
        y = self.predict(x)

        return cross_entropy_error(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy


    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}

        batch_num = x.shape[0]


        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)


        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)

        dz1 = np.dot(dy, W2.T)
        da1 = sigmoid_grad(a1) * dz1
        grads['W1'] = np.dot(x.T, da1)
        grads['b1'] = np.sum(da1, axis=0)

        return grads

最初に宣言したparamsは辞書型で、各層の重み(W)とバイアス(b)を保持するために使います。 gradは辞書型で、各層の重み(W)とバイアス(b)の勾配を保持します。

__ init__メソッドは、()入力層のニューロン数、隠れ層のニューロン数、出力層のニューロン数)を引数にとり、各値の初期化をします。

predictメソッドは、画像データを引数にとり、各層に順番に流し込んでいきます。（活性化関数はシグモイド関数、出力関数はソフトマックス関数）

lossメソッドは、(画像データ、正解ラベル)を引数にとり、損失関数(交差エントロピー誤差)を通した値を返します。

accuraryメソッドは、(画像データ、正解ラベル)を引数にとり、認識の制度を返します。

numerical_gradientメソッドは、数値微分を用いて勾配を求めます。損失関数を各ニューロンの重みで偏微分しています。途中でlamnda式を使っている箇所がありますが、この部分は self.loss(x, t)を実行する関数を宣言しているのとあまり意味は変わりません。記述がシンプルで済むので取り入れています。

gradientメソッドでは、誤差逆伝播法を使って勾配を求めます。逆伝播で求めたシグモイド関数の勾配sigmoid_gradを使っています。

２層ニューラルネットワークを使った学習の実装

上で実装した２層ニューラルネットワークを実際に使っていきます。

import sys, os
sys.path.append(os.pardir)  
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer import TwoLayerNet

numpyとmatplotlibのほかに、先ほどと同じように親ディレクトリのファイルをインポートするための設定に必要なライブラリも使っていますが、本質から外れるので説明は省きます。要は、mnist.pyがインポートできればOKです。（今回は、本でデータセットがまとめられていたのでそれをダウンロードしてそのまま使用しました。）それから、上で実装したTwoLayerNetのインポートも忘れずに行います。

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000  
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

networkを、各パラメータを指定したTwoLayerNet型のインスタンスにします。 iters_numで訓練データ数を、batch_sizeでミニバッチの数を指定します。

iter_per_epochとは、エポック（見た通り、訓練データ数/ミニバッチ数）を計算して代入しています。

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    grad = network.gradient(x_batch, t_batch)

    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))


markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))

gradに勾配の値を入れるときに、順伝播(数値微分)を用いるならnumerical_gradientを、逆伝播を用いるならgradientを使用します。

認識精度を計算する際、データ一つあたりではなく１エポックごとに精度を計算しています。（そこまで高精度な結果はいらないので）

最後に、結果（認識精度の変化）をグラフで出力します。

plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

出力結果

逆伝播：

15秒ほどでプロットまで終わりました。学習が進むにつれて損失が少なくなっている様子がわかります。また、trainデータとtestデータのグラフがほぼ重なっているので、過学習も起こっていません。

順伝播の場合は、10分ほど待っても最初のエポックの計算しか終わりませんでした。そういうものならいいけれど、何か問題があるのかな...

おわりに

参考にするとか言っておきながら、ほとんど丸コピになってしまいました... 機械学習、深層学習という分野は、初学のうちはライブラリの使い方ゲ―のようになってしまう気がしますが（僕もほとんど何も知らないので言い切れませんが）、このように自分の手で一からアルゴリズムを実装してみるのもまた楽しいです。