Rustの台頭で耳にすることが多くなった線形型(Rustのはもうちょっと条件が緩いAffine型です)だが,一体何が線形なのだろうか,と誰しも考えるだろう.今回は線形型システムの線形性について少しだけまとめてみた.
線形型システム
一言で言うと,変数の使用回数条件,"ちょうど1回呼び出される"制約をつけることができる型システムである.
簡素な線形型システムの構成
以下に具体的に線形型システムを構成する.
<toplevel> ::= let <identifier> '=' <term> ';' <toplevel>
| {empty}
<qualifier> ::= lin | un
<boolean> ::= true | false
<term> ::= <identifier>
| <qualifier> <boolean>
| <qualifier> 'lambda' <identifier> ':' <qualified-type> '.' <term>
| <term> <term>
<qualified-type> ::= <qualifier> <type>
<type> ::= Bool
| <qualified-type> '->' <qualified-type>
みたいにsyntaxを定める.
型はqualified-typeで,unかlinどちらかの修飾子がつく.
それ以外は,至る所で修飾子を書かせる以外は単純型付きラムダ計算と同じ.
un 型はふつうの単純型と同じで,lin 型が線形型とする.
以下にlin 型に対する型付け規則のうち,主要なものを示す.
コアになっているのは,文脈の分割 $\Gamma = \Gamma_1 \circ \Gamma_2$ の概念である:
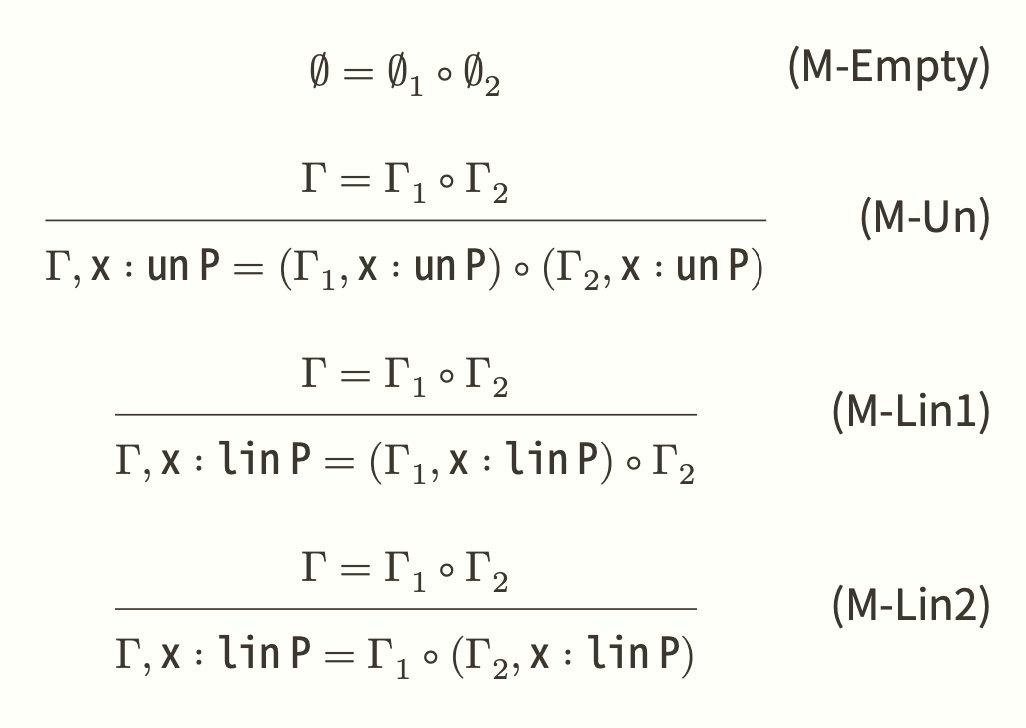
分割演算$\circ$が行われた時,un型は両側の文脈に残る(コピーされる)が,lin型はどちらか片方の文脈にしか残らない.
Appの型付け規則を見る:
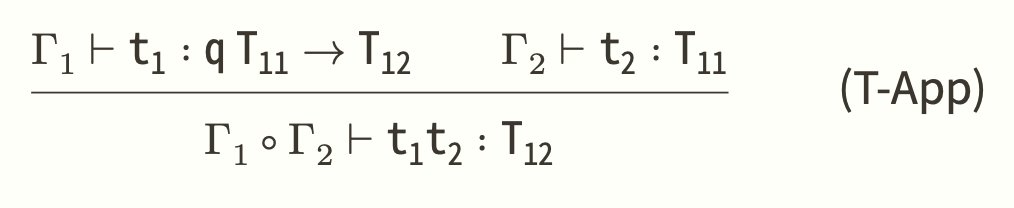
ここで,qはqualifier(lin | un)である.
関数適用の際,un型は分割の影響なく(単純型のように)型付けが進むが,lin型は,(M-Lin)により,型付けが"消費"される.
以上のように,lin 型は,一回だけ使用できる型である.
例:恒等関数
let id = lin lambda x:lin bool.x;
let main = id (lin true);
と書くと,idは,lin (lin bool -> lin bool)型の関数で,lin bool型の引数をそのまま返す.(ただの恒等関数)
mainでは,idを呼び出している.
このとき,同文脈上(同ファイル内)でもう一度idを呼ぶと型エラーになるし,一度も呼ばなくても型エラーになる.
線形型と線形論理
このように,変数の使用回数条件を付与できる型システムだが,この機能は,線形論理を基にしている.
線形論理
線形論理とは,ひとことで言うと"resource sensitive"な論理体系である.ここでのresourceとは論理式の数という,古典論理ではまず気にすることがなかった概念である.
具体例を交えて紹介する.
次のような命題をもとに,"かつ"と"ならば"について再考する.
命題A . 100 円持っている.
命題B . コーラ (100 円) が買える.
命題C . 水 (60 円) が買える.
このとき,A ならば B,や,A ならば C,が自明に成立する.
AならばBかつCはどうだろう.
古典論理なら,A$\to$B$\wedge$Cは成り立つが,日本語の意味を考えると,100円だけ持っていてもコーラと水両方を買うことはできない.
このような着眼点から,自然言語で"かつ"と記述しても,その意味は以下のような2種類に分割することができると考えられる:
-
コーラと水どちらも買う"かつ": $\otimes$
- A ならば B $\otimes$ C は成り立たない.
-
コーラと水どちらかしか買わない"かつ" : &
- A ならば B & C は成り立つ.
資源管理というから,これらの"かつ"を説明する.B & Cは,(どちらでも良いが)BとCどちらか一方を選択する.一方で,B$\otimes$Cは,BとCどちらも両方とってくることを表す.1アクションでいくつ取ってくるかの違いがある.
この時,命題は資源で,前件の資源を使って後件を実行すると考えると,後件で消費する数だけ前件に命題を書くと,論理式を成立させることができると言える.
また,"ならば"についても再考する必要がある.命題論理の$\to$には,前件の資源を消費するというニュアンスがないため,専用の含意,$\multimap$を導入する必要がある.
今までの議論は,以下の論理式で示される:
- A $\multimap$ (B & C) (成り立つ)
- A $\multimap$ (B & C) (成り立たない)
- (A $\otimes$ A) $\multimap$ (B $\otimes$ C) (成り立つ)
詳細
以下に,線形論理の推論規則を示す.

$\oplus$,
contraction,weakeningが,演算子'!','?'の上でのみ定義されている.contraction,weakeningは,論理式の任意個コピーを可能にしている.(exchangeは認められている.$\Gamma$は論理式の列で,exchange,contraction,weakeningがあると,集合のように振る舞う.一方で,exchangeのみだと,$\Gamma$は多重集合のように振る舞う.) つまり,デフォルトでは線形論理式はresource sensitiveで,これらの演算子をつけた時のみ資源の消費を考慮しなくてもよくなる. これらの演算子は指数的演算子と呼ばれていて,線形論理と古典論理を接続している.
線形論理の線形性
やっと本題に入る.線形型の線形性は線形論理の線形性である.なぜ線形論理は線形論理と呼ばれるのか.
その答えは,線形論理の誕生まで遡る.
線形性の発見,超大雑把な概要
(各種定義は,元気があったらまとめます.)
線形論理は,1987年にGirardというおじさんが発見し,発表した.
Girardは当時,直観主義論理の分析を行っていた.その過程で,論理演算子が2種類に分解できることを発見した.これが,線形論理の大元である.
また,Girardは,発見した論理体系における手続きを,coherent space(単なる無向グラフ)上でモデル化し,分析した.Scottの領域理論では,型は位相空間で,関数は位相空間上の連続写像だった.一方で,Girardは,型をcoherent space,関数をcoherent space上のstable な写像だと定義した.coherent spaceを持ち出した理由は,色んなものを色んなもののクリークとして説明したかったからだと勝手に解釈している.
そして,線形論理の特徴である,単一呼び出し性を持つ手続きをcoherent space上の写像として定義すると,その写像が線形性(のような特性)を持つことを発見した.
これが,線形論理の線形性の所以である.変数の呼び出し回数制限として現れている,単一呼び出し性が,線形性に対応している.
もう少し詳しく
WIP.
詳しい定義はhttps://www.kurims.kyoto-u.ac.jp/~terui/birth.pdfをみてください.
https://ziphil.com/diary/mathematics/71.htmlも参考になります.
まとめ
線形型システムの線形性は線形論理の線形性で,単一呼び出し性を線形性と呼んでいるが,詳細は領域理論の話になって難しい.
